Collision of Point Masses with Rigid Bodies

Five identical balls each of mass $m$ and radius $r$ are strung like beads at random and at rest along a smooth, rigid horizontal thin road of length $L$, mounted between immovable supports. Assume $10r<L$ and that the collision between balls or between balls and supports are elastic. If one ball is struck horizontally so as to acquire a speed $v$, the average force felt by the support is

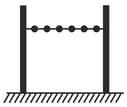
A uniform rod of mass $M_1$ is hinged at its upper end as shown in the figure. A particle of mass $M_2$ which is moving horizontally strikes the rod elastically at its midpoint. If the particle comes to rest after collision, then if the value of $\frac{M_1}{M_2}=\frac{n}{8}$ what is the value of $n$?

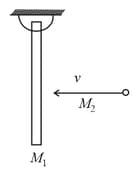
A bullet of mass $m$ is fired horizontally into a large sphere of mass $M$ and radius $R$ resting on a smooth horizontal table.

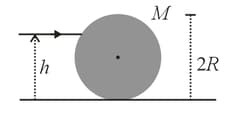
The bullet hits the sphere at a height $h$ from the table and sticks to its surface. If the sphere starts rolling without slippng immediately on impact, then

A rod $\mathrm{AB}$ of mass $\mathrm{M}$ and length $\mathrm{L}$ is lying on a horizontal frictionless surface. A particle of mass $\mathrm{m}$ travelling along the surface hits the end $\mathrm{A}$ of the rod with a velocity ${\mathrm{v}}_0$ in a direction perpendicular to $\mathrm{AB}$. The collision is perfectly elastic and after the collision, the particle comes to rest. The ratio $\frac{\mathrm{m}}{\mathrm{M}}$ is

A uniform rod of mass $m$ and length $2a$ lies at rest on a smooth horizontal table. A perfectly elastic particle of same mass $m$, moving with speed $v$ on the table in a direction perpendicular to the rod, strikes one end of the rod. The kinetic energy generated in the rod is

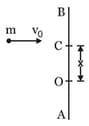
A uniform road AB of length L and mass M is lying on a smooth table. A small particle of mass m strikes the rod with a velocity v₀ at point C a distance x from the ccentre O. The particle comes to rest after collision. The value of x, so that point A of the rod remains stationary just after collision is